전형준

Variational Autoencoder

안내글

본 글은 NAVER D2의 ‘오토인코더의 모든 것’ 강의 영상을 보며 Variational Autoencoder에 대해서 이론과 학습부분을 정리한 글입니다. 정리간에 제가 직관적으로 이해가 가지 않는 부분들 역시 추가로 같이 정리하였습니다. 만약에 이상한 부분이 있다면 언제든지 댓글로 피드백바랍니다.

AutoEncoder와의 차이점

: 학습 목적이 다르다!

AutoEncoder는 매니폴드 러닝을 위하여, 모델의 구조중 앞단(Encoder)를 학습하는 것이 목적이다.
Variational Autoencoder는 생성모형으로써 데이터를 생성한다. 이를 위해서 모델의 구조중 뒷단(Decoder)를 학습하는 것이 목적이다.

특징

A. 생성모형으로써 데이터를 생성한다.

생성모형

위와 같은 생성기(deep learning model)가 있을 때, 생성기는 z라는 잠재변수를 입력으로 받고 데이터 x를 생성한다. 이때, Variational AutoEncoder를 이해하기위해서, 확률론적 관점으로 생성기를 바라보야한다. 우선 잠재변수 z가 특정분포 $p(z)$에서 샘플링된 값이라고 가정하면, 아래와 같이 표현된다.

$z \sim p(z)$

생성기는 이 잠재변수를 입력으로 가지고, 데이터의 파라미터 $\theta$를 출력하는 결정론적인(deterministic) 함수 $g_{\theta}$로 여겨진다. 여기서 결정론적이란 의미는 정해진 입력과 파라미터에 대해서 항상 같은 답을 내놓는다는 뜻이다.

$\theta = g_{\theta}(z)$

또한 이 잠재변수 z에 대해서 대응되는 실제 데이터 $\hat{x}$(모델이 생성하고자 하는 데이터)와 이상적으로 출력되는 데이터의 파라미터 $\hat{\theta}$가 있다면, 데이터가 정규분포이고 파라미터가 평균 일 때 아래의 식이 성립할 것이다. 그리고 이 $\hat{x}$은 잠재변수 z에 대해서 정해진 값으로써, 확률변수가 아닌 실제 관측할 수 있는 값이다.

$\hat{x} = \hat{\theta} $ (평균이기 때문에..)

잠재 변수 z에 대해서 모델의 출력이 $g_{\theta}(z)$ 이라면, 아래와 같이 실제 데이터$\hat{x}$가 나올 가능도(likelihood)를 구할 수 있다.

$ likelihood : p(\hat{x}|g_{\theta}(z)) = p(\hat{x}|x)$

이러한 가능도는 아래의 그림과 같이 구해지며, 만약에 출력된 $\theta$(ex.평균)로 만들어진 x의 확률분포가 실제 $\hat{x}$를 잘 반영한 분포라면, 다음과 같이 가능도가 높을 것이다.

가우시안 분포 x가 점차 $\hat{x}$의 가능도를 높히는 과정

그래서 생성모델을 학습할 때는 전체 데이터에 대해서 이 가능도를 최대화하도록 모델의 파라미터를 학습하고(Maximum Likelihood), 그 결과 파라미터 $\theta$는 $\hat{\theta}$에 가까워진다. 이때, 앞에서도 말했지만 $\theta$는 데이터가 가우시안분포일 경우 평균이나 표준편차가 된다.

($\theta \rightarrow \hat{\theta}$)

만약에 해당 $\theta$ 값을 잘 구하게된다면, 다음과 같이 marginalize를 하여 데이터 전체의 분포도 구할 수 있다. 왜냐하면 p(z)는 미리 정해둔 값이고, $g_\theta(z)$는 모델에 의해서 학습된 출력이기 때문이다.

$p(x) = \int p(x|g_\theta(z))p(z)dz$

B. 잠재변수의 사전분포 p(z)가 제어기역할을 한다.

만약에 generator의 출력이 이미지라면, 임의의 출력도 좋지만 보통은 출력된 이미지의 종류를 조정할 수 있기를 원한다.(ex. 사람 얼굴이라면, 성별, 머리색등의 조종) 입력 z는 그러한 출력을 조종하는 역할로 사용될 수 있다. 그래서 보통 z값 자체를 사용하기 쉽게하기 위해서, 정규분포로 사전분포 p(z)를 정한다. 하지만 latent space를 임의분포로 만드는 것은 실제 데이터 분포를 잘 표현하지 못할 수 있다. 하지만 생성기의 레이어를 거치면서 잘나타내도록 바꿀 수 있다.

C. 생성기만 있다면, 직접적인 MLE를 통한 학습은 불가능하다.

만약에 생성기의 출력이 가우시안분포의 파리미터 라면,아래와 같이 가능도는 음의 로그가능도에 반비례하고, 이것은 데이터 x와 $g_{\theta}(z)$사이의 거리에 비례하게된다.

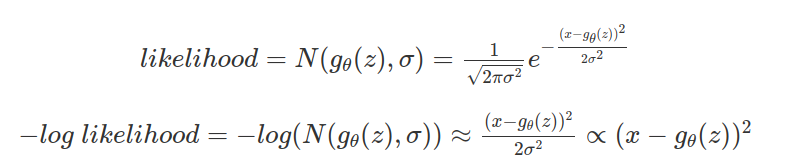
즉 학습간에 mean-square error(MSE)를 사용하여 음의 로그가능도를 줄이는 쪽으로 학습하게된다. 하지만 이 경우 아래와 같이 이미지를 출력하는 네트워크의 경우, 원본이미지 (a)에 대해서 일부 출력이 안되는 이미지(b)보다 위치만 약간 다른 이미지(c)가 의미론적으로 숫자 2에 가깝지만, MSE는 더 크기 때문에 (b)이미지로 학습될 수 있다. 이렇게되는 원인에는 임의로 정한 z의 분포가 x를 잘 나타내지 못하기 때문이다.그래서 MLE만을 사용해서는 학습이 (b)처럼 될 가능성이 있다.

D. z를 p(z)에서 샘플링하는 것이 아니라, p(z|x)에서 샘플링하는 특징을 가진다.

prior(p(z))에서 z를 샘플링하는 것이 아닌 어떤 이상적인 샘플링함수(아래의 식과 같은)를 사용해야 학습간에 이런 문제를 해결할 수 있다. 이 샘플링함수는 데이터를 잘 생성하기위해서 x라는 evidence가 주어진다.

$p(z|x) \approx q_\phi (z|x) \sim z $

당연히 이러한 이상적인 샘플링함수를 알지 못하기때문에, 이 샘플링함수(확률분포)를 추정하기 위해서 variance inference를 사용한다. 그 결과 우리가 아는 분포의 형태를 가지는 함수 $q_\phi(z / x)$를 샘플링함수로 구할 수 있다.

Variance Inference

알 수 없는 정답 분포 $p(z/x)$를 얻기위해서, 근사적으로 우리가 알고 있는 분포의 형태(가우시안)을 가지는 $q_\phi(z / x)$를 정답분포에 가깝게 학습시키는 방식

결국 x를 잘나타내는 z의 샘플링함수를 구하고(variance inference), 이로부터 생성기를 MLE로 학습하여 데이터의 분포(p(x))를 구할 수 있다.

E. VAE의 에러함수는 variance inference와 MLE가 합쳐져있다.

최종적으로 학습에 관련있는 것은 다음 세가지이다.

$p(x)$ : 구하고자 하는 데이터의 정답 분포(고정됨, 알지못함)
$p(z/x)$ : 데이터를 잘 나타내는 이상적인 샘플링함수(고정됨, 알지못함)
$q_\phi(z / x)$ : 파리미터 $\phi$에 의해서 학습되며, $p(z/x)$에 근사해지는 함수

학습에 사용되는 에러함수의 유도는 다음과 같다. 식 (1)은 Jensen의 Inequality에 의해서 log가 적분식 안으로 들어고 부등식이 성립한다.(Jensen’s Inequality :$f(E[x]) \geq E[f(x)]$)

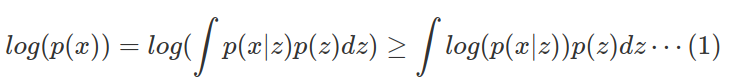
이제 우리가 알고있는 $q_\phi(z / x)$ 식에 대입하면 식 (2)를 구할 수 있다. p(x)는 부등식의 우항보다 항상 크게된다.

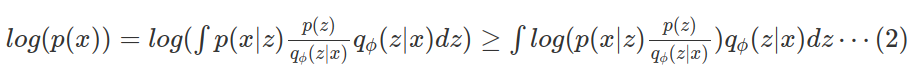
이 우항을 정리하면 최종적인 식(3)이 나오게된다. 이 식(3)을 $ELBO(\phi)$ 라고한다. 이 ELBO를 최대화 하는 $\phi*$를 찾으면 좋은 z의 샘플링 모델을 구하게된다.

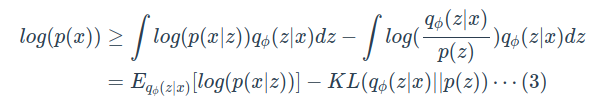
또다른 유도방법에는 등식의 형태로 구하는 것이 있다. 식(4)는 $\int q_\phi(z/x)dz=1$을 만족하기 때문에 성립한다.

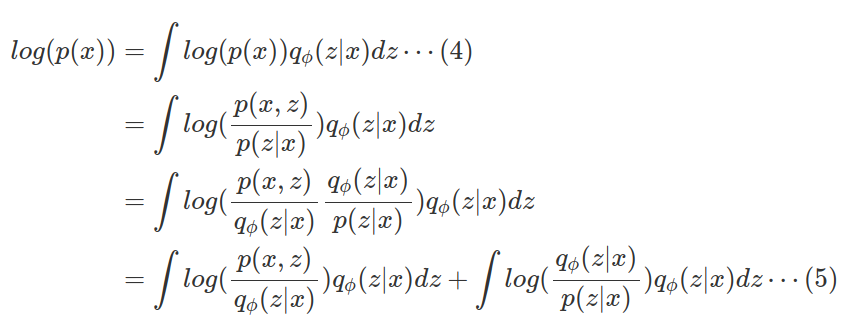
식을 정리하면 식 (5)와 같이 나오는데, 첫번째 항은 식(3)을 정리한 $ELBO(\phi)$ 식이고, 두번째 항은 $q_\phi(z / x)$와 $p(z/x)$사이의 KL-divergence(두 분포사이의 거리)이다. KL-divergence는 항상 0보다 크거나 같기 때문에, $ELBO(\phi)$는 $log(p(x))$보다 작거나 같다.

최적화과정에서 KL을 최소화하는 $q_\phi(z / x)$를 찾으면 되는데, $p(z / x)$라는 값은 모르기때문에 KL을 구할 수가 없다. 그래서 대신에 $ELBO(\phi)$를 최대화하는 $\phi$를 찾는다.

이 $ELBO(\phi)$ 식을 다시 정리하면 아래와 같다.

그래서 결국 최종적으로 최적화문제는 2가지가 된다.(좋은 샘플링함수$q_\phi(z / x)$를 구하는 것, 생성기의 출력파라미터가 데이터를 잘나타내는 것)

정리하면 아래와 같다.

1 Optimization problem 1 on $\phi$ : Variance Inference

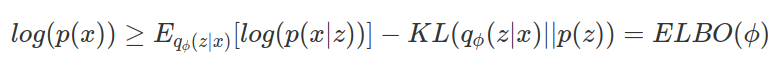
2 Optimization problem 2 on $\theta$ : Maximum Likelihood

( 1번의 최적화식의 양변에 -를 곱하고 x의 원소합의 형태로 바꾸고, 실제 z가 x에 영향을 주는 $g_\theta(z)$로 바꾼다.)

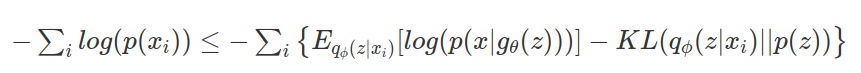
두번째 식의 경우 우항의 첫번째 항이 minus log- Likelihood의 형태를 가지게된다. 그래서 이 $ELBO(\phi)$식에는 Variance Inference의 최적화식뿐만아니라 maximum likelihood식이 같이 포함되어있는 셈이다. 최종적인 최적화는 다음과같다.

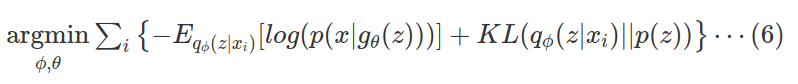
이것을 모델 관점에서 보면, 아래의 사진과 같이 모델의 인코더(Inference Network)는 z를 샘플링하기 위한 분포의 파라미터를 제공하고, 디코더(Generation Network)는 데이터를 생성하기위한 모델의 파라미터를 제공한다. 그리고 이에따라서 실제 모델의 구조는 오토인코더와 같지만 수식적으로 관계는 없다.

식 (6)의 에러항을 분석해보면 다음과 같다.

$-E_{q_\phi(z | x_i)}[log(p(x|g_{\theta}(z)))]$

Reconstruction Error
현재 샘플링 함수에 대한 음의 로그 가능도를 나타냄
$x_i$에 대한 복원 오차

$KL(q_\phi(z | x_i)||p(z))$

Regularization term
$q_\phi(z / x_i)$는 variational inference에서 $p(z/x)$의 추정에 사용되는 함수
$p(z)$는 KL-divergence값을 구하기 쉬워야한다.또한 $q_\phi(z / x_i)$의 분포가 점차 prior에 가까워지게한다.(샘플링이 쉬워진다.)
$p(z)$는 z의 분포를 고정시킨다.

F. VAE의 학습과정.

자세한 내용은 ‘VAE의 학습과정’을 보길바란다.

학습과정은 다음과 같은 step을 가진다.

(예시)

가정 1. 인코더의 출력을 가우시안분포의 파라미터이다.($q_\phi(z / x_i)$의 분포를 가우시안이라고 가정)

가정 2. p(z)의 분포 역시 다루기쉬운 가우시안 분포라고 가정

step 1. 데이터를 인코더의 입력으로 넣어서, 평균과 분산의 파라미터를 얻는다.

step 2. 이전 step에서 출력된 파라미터를 가지는 분포와 사전 분포 $p(z)$ 사이의 KL-divergence를 구한다.($KL(q_\phi(z / x_i)||p(z))$) 이때, 두 분포가 가우시안이면 KL-divergence를 구하기 쉽다!

step 3. 이제 $E_{q_\phi(z / x_i)}[log(p(x/g_\theta(z)))]$를 구해야하는데, 모든 z에 대해서 평균을 구하는 것은 어렵기 때문에 아래와 같이 monte-carlo 기법을 활용한다. 이 방법으로 $q_\phi(z / x_i)$에서 샘플링된 $z_i$의 평균을 사용한다.

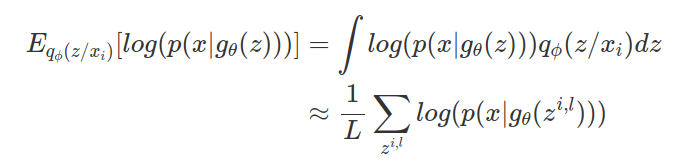
가령 $g_\theta(z)$의 파라미터를 가우시안의 파라미터로 잡으면 전체 학습과정은 다음과같다.

$g_\theta(z)$를 베르누이분포등으로 가정하는 것 등의 예시는 영상에 나와있지만, 비슷한 내용이기 때문에 생략한다.

G. Manifold learning이 가능하다.

p(z)를 두었기 때문에, 아래의 그림처럼 매니폴드 영역(2차원 공간)에서 AE와 달리 p(z)의 분포를 따라가는 것을 볼수있다.(가우시안) 이로인해서, 샘플링등이 좋아지는 특징을 가진다.